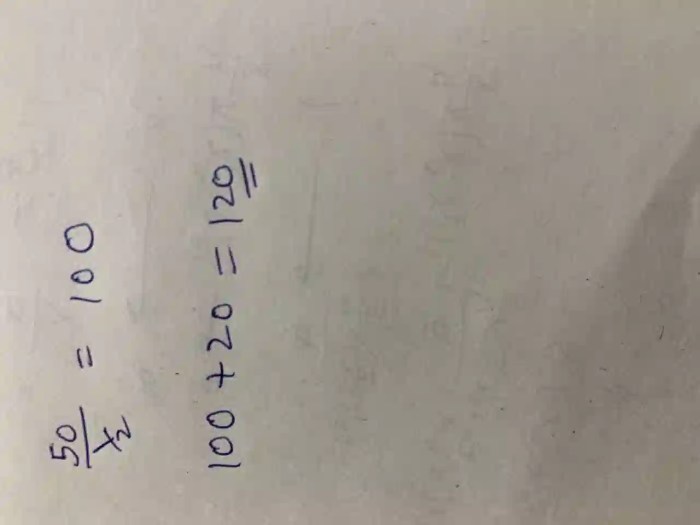Embark on a mathematical adventure as we delve into the enigmatic expression “four less than half a number.” This concept, seemingly simple yet surprisingly versatile, holds secrets that we shall unravel together.
Join us as we navigate the algebraic maze, uncover real-world applications, and explore captivating variations. Along the way, we’ll illuminate the path to solving this enigmatic equation, leaving no stone unturned.
Mathematical Representation

The mathematical expression “four less than half a number” can be represented algebraically as:
(1/2)n- 4
where nrepresents the unknown number.
Examples, Four less than half a number
- If nis 10, then (1/2)n – 4 = (1/2) – 10 – 4 = 5 – 4 = 1.
- If nis 20, then (1/2)n – 4 = (1/2) – 20 – 4 = 10 – 4 = 6.
Algebraic Manipulation: Four Less Than Half A Number

To isolate the unknown number, we’ll perform algebraic operations on both sides of the equation.
Step 1: Isolate the term with the unknown number
First, let’s get rid of the constant term (-4) on the left side by adding 4 to both sides:
4
– 4< half a number = 4 + 4
This simplifies to:
half a number = 8
Step 2: Divide both sides by the coefficient of the unknown number
Now, we need to isolate the unknown number. The coefficient of the unknown number is 1/ 2. To get rid of the fraction, we’ll multiply both sides by 2:
- 2
- half a number = 2
- 8
This simplifies to:
a number = 16
Real-World Applications
The expression “four less than half a number” is a mathematical concept that can be applied to various real-world scenarios. It helps us model and solve practical problems involving quantities or measurements.
Calculating Discounts
In the context of discounts and sales, we often encounter situations where a percentage discount is offered on a product or service. To calculate the discounted price, we can use the expression “four less than half a number.” Let’s say a product is originally priced at $100 and a 20% discount is being offered.
The discount as a fraction of the original price is 20% or 0. 2. Four less than half of the original price can be expressed as:
$$(1/2)
- 100
- 4 = 46$$
Therefore, the discounted price would be $100 – $46 = $54.
Measuring Ingredients
In cooking and baking, recipes often specify ingredient quantities as a fraction or percentage of a larger amount. For example, a recipe may call for “half a cup of flour minus four tablespoons.” This is equivalent to the expression “four less than half a number.”
Let’s say the recipe requires 1 cup of flour. Half of 1 cup is 1/2 cup. Four less than 1/2 cup is:
$$(1/2)
- 1
- 4 = 1/2
- 4 =
- 3 1/2$$
However, since we cannot have negative quantities of ingredients, we interpret this result as zero. Therefore, we would use 0 cups of flour for this recipe.
Determining Age Differences
In everyday conversations, we may encounter situations where we need to compare ages or age differences. The expression “four less than half a number” can help us solve such problems.
For example, if you know that your friend is four years less than half your age, and you are currently 28 years old, you can use this expression to find your friend’s age.
Half of your age is 28/2 = 14. Four less than half your age is:
$$14
4 = 10$$
Therefore, your friend is 10 years old.
Extensions and Variations

The expression “four less than half a number” can be modified to create variations that explore different mathematical concepts. These variations include:
Four More Than Half a Number
This variation, “four more than half a number,” involves adding four to half the value of an unknown number. The mathematical representation is:
(1/2)n + 4
Four less than half a number is a tricky concept, but it’s related to a crossword clue: rule by one . This clue refers to a situation where a single rule governs something, just like the rule that you must subtract four from half a number to find its value.
where n represents the unknown number.
Half a Number Minus Four
This variation, “half a number minus four,” involves subtracting four from half the value of an unknown number. The mathematical representation is:
(1/2)n
4
where n represents the unknown number.
These variations demonstrate the flexibility of mathematical expressions and how they can be adapted to represent different scenarios. The mathematical principles discussed earlier, such as algebraic manipulation and real-world applications, apply equally to these variations.
Graphical Representation
A graphical representation can provide a visual understanding of the relationship between the unknown number and the expression “four less than half a number.” We can create a table or a graph to illustrate this relationship.
The following table shows the values of the unknown number (x) and the corresponding values of the expression “four less than half a number”:
| x | Four less than half a number |
|---|---|
| 2 | 0 |
| 4 | 1 |
| 6 | 2 |
| 8 | 3 |
| 10 | 4 |
We can also plot these values on a graph to create a line graph. The x-axis of the graph represents the unknown number (x), and the y-axis represents the value of the expression “four less than half a number.” The line graph will show a linear relationship between x and the expression.
Using the Graph to Solve the Equation
The graph can be used to solve the equation “four less than half a number” for different values of the unknown number. To do this, we can find the x-intercept of the graph, which is the point where the line crosses the x-axis.
The x-intercept represents the value of x for which the expression “four less than half a number” is equal to zero.
For example, if we want to find the value of x for which the expression “four less than half a number” is equal to 2, we can locate the point on the graph where the line intersects the horizontal line y = 2. The x-coordinate of this point is the value of x that satisfies the equation.
FAQ Explained
What is the mathematical representation of “four less than half a number”?
(1/2)n – 4
How do I isolate the unknown number in the expression?
Multiply both sides by 2 and add 4 to both sides.
Can you provide an example of a real-world application of this expression?
Calculating the number of days left in a month that is four days shorter than half the year.